El dilema del prisionero
Publicado el 10 de diciembre de 2024
El dilema del prisionero es un problema clásico en la teoría de juegos que ilustra cómo las decisiones individuales, tomadas en busca del interés propio, pueden llevar a resultados perjudiciales para todas las partes. Este dilema tiene connotaciones psicológicas, filosóficas y tecnológicas, por lo que exploraremos dónde y cómo interviene cada área. Este dilema fue formulado por Merrill Flood y Melvin Dresher, dos matemáticos de la RAND Corporation, organización dedicada al análisis estratégico durante la guerra fría, y Albert W. Tucker (Teórico de juegos) le dio la forma narrativa estándar que se conoce hasta hoy.
Narrativa
Se arresta a dos criminales, prisionero 1 y prisionero 2, en celdas separadas donde no tienen un intercambio de información. Se les da a ambos prisioneros dos opciones a elegir: traicionar (delatar al otro prisionero) o cooperar (quedarse callado), y dependiendo de lo que elijan se les dará una sentencia. A continuación la matriz de decisiones:
| (2) , (1) | Traición | Cooperación |
| Traición | Sentencia intermedia para ambos | (1) sentencia larga, (2) queda libre |
| Cooperación | (2) sentencia, (1) queda libre | Sentencia leve para ambos |
Podemos modificar este modelo propuesto por Albert Tuck para facilitar las simulaciones, usando números enteros en vez de sentencias y añadiendo un determinado número de iteraciones:
Existe un banquero con un cofre de monedas de oro que invita a dos personas a enfrentarse en un juego. De la misma manera, no hay comunicación entre ambas personas pero cambiamos ligeramente las decisiones a tomarse: cooperar y no cooperar, donde el ganador se decide por la mayor cantidad de monedas adquiridas, quedando la matriz de decisiones de la siguiente manera:
| (2) , (1) | No cooperar | Cooperar |
| No cooperar | Una moneda a cada uno | Recibe 5 monedas el que no coopero |
| Cooperar | Recibe 5 monedas el que no coopero | 3 monedas a cada uno |
Trivialmente la mejor manera de ganar en la modalidad de una sola iteración es siempre traicionar, ya que en este modelo, traicionar siempre da mayor o igual ganancia que cooperar, sin importar lo que el otro jugador decida hacer. A una situación donde ambos jugadores se dieran cuenta que traicionar siempre trae un mayor beneficio y ambos lo aplicaran en el juego, se le llama Equilibrio de Nash, ya que no hay incentivos externos para cambiar la estrategia.
Sin embargo, en muchas situaciones cotidianas no hay una sola iteración, ni tampoco solo dos jugadores, como las relaciones sentimentales, de trabajo, en los negocios, en la competencia económica, política, incluso ecosistemas naturales donde existen relaciones simbióticas en las que muchas especies dependen de la cooperación para su supervivencia. Entonces en esta modalidad, ¿cuál sería la mejor estrategia para ganar?
Robert Axelrod organizó una competencia mundial en los años 80 para estudiar estrategias en el dilema, donde los participantes programaron algoritmos para jugar múltiples rondas. Su objetivo era investigar cómo surge y se mantiene la cooperación en un mundo donde los individuos actúan bajo su propio interés. Se recibieron estrategias de una variedad de disciplinas, desde psicología y economía hasta teoría de juegos. Algunas estrategias eran muy simples, mientras que otras eran complejas y basadas en patrones o cálculos probabilísticos.
- Tit-for-Tat (Ojo por ojo): Comienza cooperando y luego imita la acción previa del oponente.
- Always Defect: Traiciona en cada ronda.
- Always Cooperate: Coopera sin importar la acción del oponente.
- Grudger: Coopera hasta que el oponente traiciona, luego traiciona para siempre.
- Random: Actúa al azar, sin un patrón definido.
- Forgiving Tit-for-Tat: Similar a Tit-for-Tat, pero tiene un 20% de probabilidad de perdonar una traición y cooperar en la siguiente ronda.
- Pavlov: Repite su último movimiento si obtuvo una recompensa alta, cambia si la recompensa fue baja. Comienza cooperando.
- Cooperate then Defect: Coopera en las rondas pares y traiciona en las rondas impares.
- Win Stay Lose Shift: Mantiene su último movimiento si la recompensa fue alta (≥3). Cambia de movimiento si la recompensa fue baja.
Gracias al aporte computacional se pudo realizar una simulación compuesta por 1000 rondas. Escrito usando Neovim, Python y POO, el código de la simulación estará en mi repositorio por si quieren modificarlo o cerciorarse de la información.
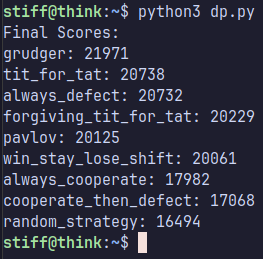
Aparentemente las posiciones quedarían así:
- Grudger
- Tit-for-Tat
- Always Defect
- Forgiving Tit-for-Tat
- Pavlov
- Win Stay Lose Shift
- Always Cooperate
- Cooperate then Defect
- Random
Y digo aparentemente por la poca cantidad de estrategias puestas en simulación, pero nos puede dar una idea para armar la siguiente tabla, usando también información de The Evolution of Cooperation, artículo escrito por Robert Axelrod y William Hamilton.
| Estrategia | Psicología | Filosofía |
|---|---|---|
| Tit-for-Tat | Promueve confianza y reciprocidad. | Refleja un equilibrio entre ética utilitaria y moral kantiana. |
| Always Defect | Explora el egoísmo y el riesgo de traición. | Representa el dilema del egoísmo racional Hobbes. |
| Always Cooperate | Examina el altruismo y la vulnerabilidad. | Modelo de contrato social o moralidad absoluta. |
| Grim Trigger | Estudia la rigidez emocional. | Aborda el debate entre castigo y perdón. |
| Random | Refleja decisiones bajo incertidumbre. | Relacionado con el libre albedrío. |
Para Axelrod, el dilema del prisionero va más allá de ser solo un problema teórico; es una herramienta útil para entender cómo funcionan las dinámicas humanas de cooperación y competencia. En diferentes escenarios y con varias iteraciones, se ha demostrado que el éxito no depende únicamente de ser egoísta o altruista, sino de encontrar un balance flexible y adaptativo entre ambos enfoques.
Las estrategias que tienen más éxito en este dilema nos muestran que:
- Comenzar cooperando ayuda a generar confianza y fomenta relaciones donde ambos lados pueden beneficiarse.
- Responder con reciprocidad refuerza estas relaciones, premiando las buenas acciones y desmotivando comportamientos desleales.
- Ser adaptable es clave para ajustarse a situaciones cambiantes y manejar posibles errores o malentendidos.
- El perdón, cuando se aplica de forma razonable, permite reconstruir relaciones tras un conflicto, mientras que la firmeza es necesaria para evitar que los demás se aprovechen.
Estas ideas no solo se quedan en teoría, sino que tienen aplicaciones prácticas en la vida cotidiana, desde relaciones personales hasta decisiones en política, economía o ecología. En un mundo donde los intereses individuales muchas veces chocan con los colectivos, este dilema nos recuerda lo valioso que es buscar estrategias que impulsen la cooperación sin perder de vista nuestros propios objetivos.
Al final, este problema nos enseña que no existen soluciones únicas o inflexibles. El verdadero éxito está en aprender, adaptarse y evolucionar según el entorno y las decisiones de los demás. Este enfoque no solo da buenos resultados en el largo plazo, sino que también ayuda a construir sistemas más justos y balanceados.